1、相邻问题捆绑法

题目中规定相邻的几个元素捆绑成一个组，当作一个大元素参与排列。

例题

有A，B，C，D，E，五个人并排站成一排，如果A，B必须相邻且B在A的右边，那么不同的排法种数有（     ）

A、60种

B、48种

C、36种

D、24种

2、相离问题插空排

元素相离（即不相邻）问题，可以先把无位置要求的几个元素全排列，再把规定的相离的几个元素插入上述几个元素的空位和两端。

例题

七个人并排站成一行，如果甲和乙两个人必须不相邻，那么不同的排法种数是（     ）

A、1440种

B、3600种

C、4820种

D、4800种

3、定序问题缩倍法

在排列问题中限制某几个元素必须保持一定的顺序，可以用缩小倍数的方法。

例题

有A，B，C，D，E，五个人并排站成一排，如果B必须站在A的右边（A，B可以不相邻），那么不同的排法种数是（     ）

A、24种

B、60种

C、90种

D、120种

4、标号排位问题分步法

把元素排到指定位置上，可以先把某个元素按规定排入，第二步再排另一个元素，如此继续下去，依次即可完成。

例题

将数字1，2，3，4填入标号为1，2，3，4的四个方格里，每格填一个数，则每个方格的标号与所填数字均不相同的填法有（     ）

A、6种

B、9种

C、11种

D、23种

解析：先把1填入方格中，符合条件的有三种方法；第二步把被填入方格的对应数字填入其它三个方格中，又有三种方法；第三步填余下的两个数字，只有一种填法，所以共有3×3×1＝9种填法，答案选B。

5、有序分配问题逐分法

有序分配问题指把元素分成若干组，可以用逐步下量分组法。

例题

有甲乙丙三项任务，甲任务需要2人承担，乙和丙任务各需要1人承担，从10个人里选出4人承担这三项任务，不同的选法种数是（     ）

A、1260种

B、2025种

C、2520种

D、5040种

6、全员分配问题分组法

例题

四名优秀学生全部保送到三所学校去，每所学校至少去一名，则不同的保送方案有多少种？

7、名额分配隔板法

例题

10个三好学生名额分到7个班级，每个班至少有一个名额，有多少种不同的分配方案？

8、限制条件的分配问题分类法

例题

某高校从某系的10名优秀毕业生中选4人分别到西部4个城市去参加中国西部经济开发建设，其中甲同学不到银川，乙同学不到西宁，共有多少种不同的派遣方法？

9、交叉问题集合法

某些排列组合问题几部分之间有交集，可以用集合中秋元素个数公式n（A∪B） = n（A） + n（B） - n（A ∩ B）

例题

从6名运动员中选出4人参加4×100米接力赛，如果甲运动员不跑第一棒，乙运动员不跑第四棒，共有多少种不同的参赛方案？

解析：设全集 = { 6人中任取4人参赛的排列 }，A = { 甲运动员跑第一棒的排列 }，B = { 乙运动员跑第四棒的排列 }，根据求集合元素个数的公式得，参赛方法共有：

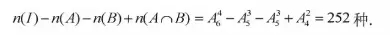
10、多元问题分类法

元素多，取出的情况也多，可以按结果要求分成不相容的几类情况分别计数，最后总计。

例题

（1）由数字0，1，2，3，4，5组成没有重复数字的六位数，其中个位数字小于十位数字的共有（     ）

A、210种

B、300种

C、464种

D、600种

（2）从1，2，3，…，100这100个数中任取两个数，使其和能被4整除的取法（不计顺序）有多少种？