在开始讲解“分类讨论”的经典例题之前，我们先来认识一下“分类讨论”这个考试必见面的忠实小伙伴，跟他打好关系的第一步，就是认识他！

所谓“分类讨论”，就是在研究和解决数学问题时，当问题所给的对象不能进行统一研究，我们就需要根据数学对象的本质属性的相同点和不同点，将对象区分为不同种类，然后逐类进行研究和解决，最后综合各类结果得到整个问题的解决，这一思想方法，我们称之为“分类讨论的思想”。

接下来我们来看看运用“分类讨论的思想”去解题的基本步骤：

 01   确定讨论对象和确定研究的全域；

 02   对所讨论的问题进行合理的分类（分类时需要做到不重复、不遗漏、标准统一、分层不越级）；

 03   逐类讨论：即对各类问题详细讨论，逐步解决；

 04   归纳总结，整合得出结论。

经典例题解析

1、已知a是实数，函数f(x)=2ax²+2x-3-a，如果函数y=f(x)在区间［-1，1］上有零点，求a的取值范围。

解析：由函数f(x)的解析式的形式，对其在定区间上零点问题的解决需要考虑它是一次函数，还是二次函数，因而需就a=0和a≠0两类情况进行讨论。

2、设函数f(x)=ln(x+a)+x²，

（1）若当x=-1时，f(x)取得极值，求a的值，并讨论f(x)的单调性；

（2）若f(x)存在极值，求a的取值范围，并证明所有极值之和大于lne/2。

解析：函数的极值、单调性是函数的重要性质。极值问题的解决，需要利用导数知识判断在该点两侧函数的单调性；而函数单调性的讨论则需要考察相应导数的符号问题。

3、设等比数列｛an｝的公比q＜1，前n项和为Sn，已知a3=2，S4=5S2，求｛an｝的通项公式。

解析：本题是数列题的基本题，“知三求二”。

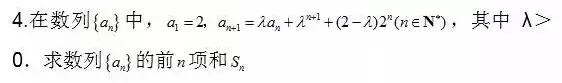
5、

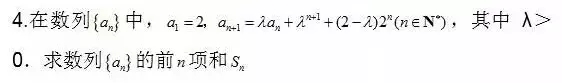
解析：圆锥曲线方程的确定要了解其中擦书字母具有的几何意义，掌握字母间的基本关系。