看完这些几何证明解题思路 几何拿高分没问题
2017-10-17 11:26
来源:
作者:
初中数学大题中的几何证明题一直是不少学生的难点,特别是那些需要学生添加辅助线才能发现思路的几何证明题。仅仅因为一条辅助线没有画出来,整整一道题的分数就可能全部丢掉。”
今天小新为大家为了总结了一些几何证明题的套路,一定能帮助同学们能够更好地解决几何证明题,把分数紧紧地握在手里!
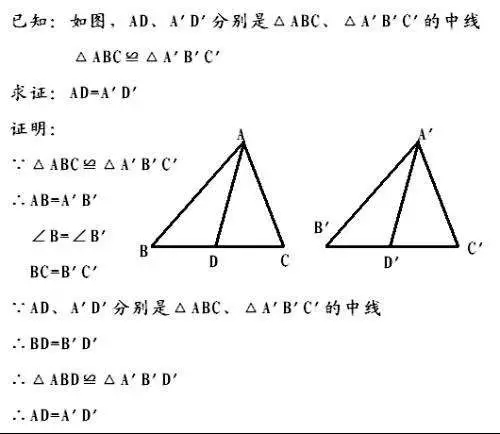
一、证明两线段相等
1、两个全等三角形中的对应边相等。
2、在同一三角形中,等角对等边。
3、等腰三角形顶角的平分线或底边上的高平分底边。
4、平行四边形的对边或对角线被交点分成的两端相等。
5、直角三角形斜边的重点到三顶点距离相等。
6、线段垂直平分线上的任意一点到线段两端距离相等。
7、角平分线上的任意一点到角的两边的距离相等。
8、过三角形一边的中点且平行于第三边的直线分第二边所成的线段相等。
9、同圆(或等圆)中等弧所对的弦或与圆心等距的两弦或等圆心角、圆周角所对的弦相等。
10、圆外一点引圆的两条切线的切线长相等,或圆内垂直于直径的弦被直径分成的两端相等。
11、两圆的内(外)公切线的长相等。
12、等于同一线段的两条切线相等。
二、证明两个角相等
1、两个全等三角形的对应角相等。
2、在同一三角形中,等边对等角。
3、等腰三角形中,底边上的中线(或高)平分顶角。
4、两条平行线的同位角,内错角或平行四边形的对角相等。
5、同角(或等角)的余角(或补角)相等。
6、同圆(或等圆)中,等弦(或弧)所对的圆心角相等,圆周角相等,弦切角等于它所夹的弧所对的圆周角。
7、圆外一点引圆的两条切线,圆心和这一点的连线平分两条切线的夹角。
8、两个相似三角形的对应角相等。
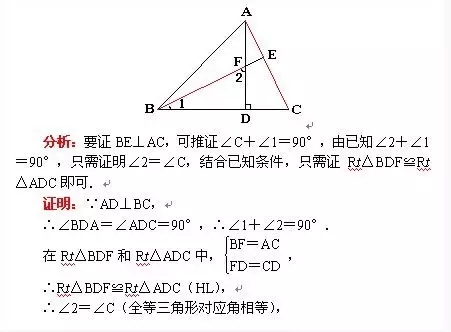
三、证明两条直线互相垂直
1、等腰三角形的顶角平分线或底边的中线垂直于底边。
2、三角形中一边的中线若等于这边一半,则这一边所对的角是直角。
3、在一个三角形中,若有两个角互余,则第三个角是直角。
4、邻补角的平分线互相垂直。
5、一条直线垂直于平行线中的一条,则必垂直于另一条。
6、两条直线相交成直角,则这两直线垂直。
7、一线端两端的距离相等的点在线段的垂直平分线上。
8、利用勾股定理的逆定理证垂直。
9、利用菱形的对角线互相垂直证垂直。
10、在圆中,平分弦(或弧)的直径,垂直于弦。
11、利用半圆上的圆周角是直角证垂直。
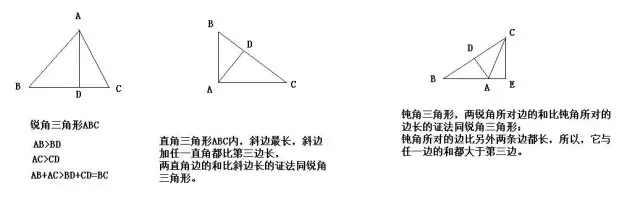
四、证明线段不等
1、在同一三角形中,大角对大边。
2、垂线段最短。
3、三角形两边之和大于第三边,两边之差小于第三边。
4、在两个三角形中,有两边分别等于而夹角不等,则夹角大的第三边大。
5、同圆(或等圆)中,弧大弦大,弦心距小。
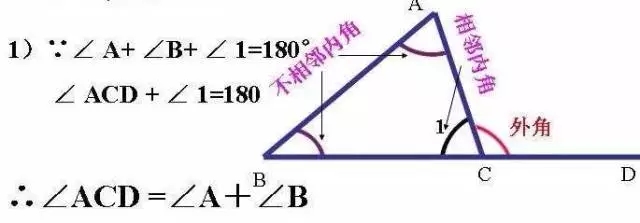
五、证明两个角不等
1、在同一三角形中,大边对大角。
2、三角形的外角大于和它不相邻的任一内角。
3、在两个三角形中有两边分别相等,第三边不等,第三边大的,两边的夹角也大。
4、同圆(或等圆)中,弧大则圆周角、圆心角大。
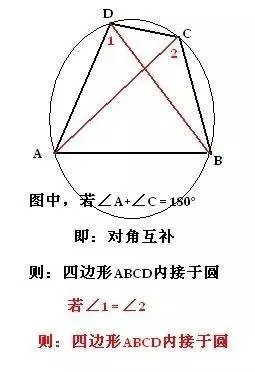
六、证明四点共圆
1、对角互补的四边形的顶点共圆。
2、外角等于内对角的四边形内接于圆。
3、同底边等顶角的三角形的顶点共圆(顶角在底边的同侧)。
4、同斜边的直角三角形的顶点共圆。
5、到顶点距离相等的各点共圆。
七、证明比例式或等积式
1、利用相似三角形对应线段成比例进行证明。
2、利用内外角平分线定理。
3、平行线截线段成比例。
4、直角三角形中的比例中项定理即射影定理。
5、与圆有关的比例定理——相交弦定理、切割线定理及其推论。
6、利用比例式或等积式化得。
看完这份几何证明题的思路总结,同学们有没有对几何证明题有了一个更清晰的解题思路呢?同学们记得要结合自己对应的情况,对这份总结进行查缺补漏哦,这样才能把几何题目的分数牢牢地握在手里!



新东方广州学校官方微信号:XDFGZXX
您可以通过公众号菜单栏【找课程】完成在线咨询、课程查询、附近
校区查找、预约试听课等操作。
焦点推荐
版权及免责声明
① 凡本网注明"稿件来源:新东方"的所有文字、图片和音视频稿件,版权均属新东方教育科技集团(含本网和新东方网) 所有,任何媒体、网站或个人未经本网协议授权不得转载、链接、转贴或以其他任何方式复制、发表。已经本网协议授权的媒体、网站,在下载使用时必须注明"稿件来源:新东方",违者本网将依法追究法律责任。
② 本网未注明"稿件来源:新东方"的文/图等稿件均为转载稿,本网转载仅基于传递更多信息之目的,并不意味着赞同转载稿的观点或证实其内容的真实性。如其他媒体、网站或个人从本网下载使用,必须保留本网注明的"稿件来源",并自负版权等法律责任。如擅自篡改为"稿件来源:新东方",本网将依法追究法律责任。
③ 如本网转载稿涉及版权等问题,请作者见稿后在两周内速来电与新东方网联系,电话:010-60908555。