八年级数学常见几何结论
2017-05-22 09:54
来源:
作者:许亚楠
几何模型是许多初中生数学学习生涯的“噩梦”,多变的题型、“任性”的辅助线和解决方法,无一不从中设置了层层阻力。今天我们就八年级出现的常见几何结论,按照类型逐一展开叙述。
01手拉手模型
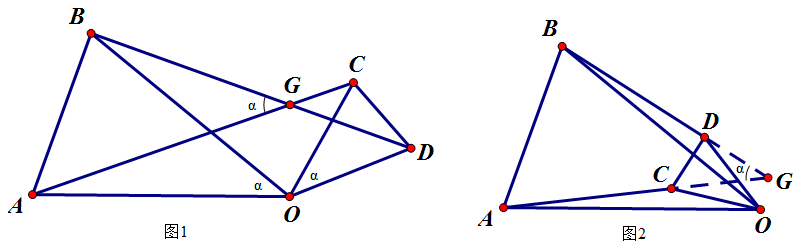
【模型条件】
1、两个等腰三角形共顶角点
2、两等腰三角形顶角相等,记作∠AOB=∠COD=α
【模型结论】
1、出现一对全等三角形,△AOC≌△BOD (SAS)
2、第三组对应边的夹角等于原三角形的顶角,即AC与BD(或延长)的夹角为α (由“8”字型可得)
【说明】
在考试中,手拉手模型中所需的等腰三角形,一般为我们所熟悉的等边三角形、直角等腰三角形.
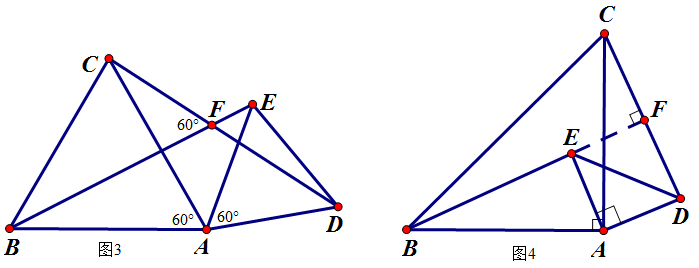
图3中的△ABC与△AED为等边三角形;图4中的△ABC与△AED为等腰直角三角形
1、两图都有△BAE≌△CAD;
2、图3中有BE与CD(或延长)的夹角为60°;图4中有BE与CD垂直(等腰直角三角形的顶角为90°).
02等腰三角形的等面积模型
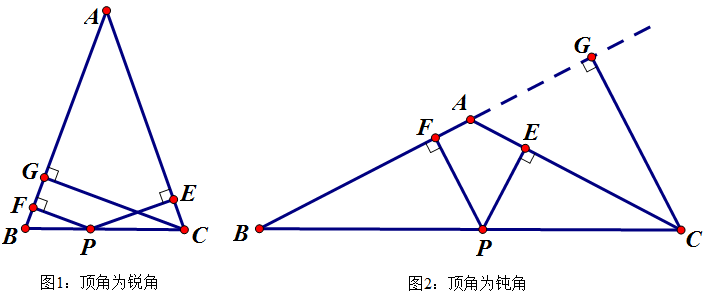
【模型条件】
1、点P是等腰△ABC底边BC上的任意一点
2、点P朝两腰作垂线段PE、PF;线段CG是一腰上的高
【模型结论】
CG=PE+PF
【推导过程】
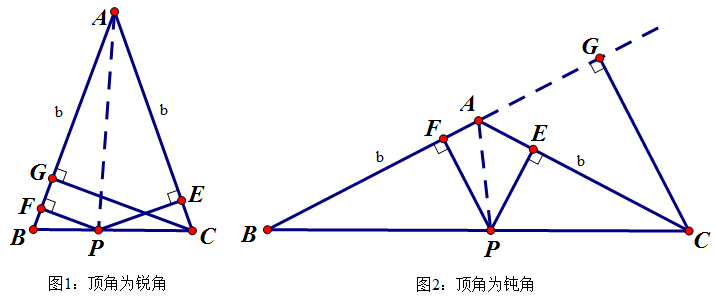
证明:连结AP,并设等腰△ABC的腰长为b
S△ABC=S△ABP+S△ACP=b·PF+b·PE=b·CG ∴CG=PF+PE
【小结】
等腰三角形底边上的一点到两腰的距离之和,等于腰上的高.
03双角平分线模型

【模型条件】
图1:PB、PC分别是∠B、∠C的角平分线
图2:PB、PC分别是∠B、∠C的外角平分线
图3:PB是∠B的角平分线、PC是∠C的外角平分线
【模型结论】
图1:∠P=90°+∠A;
图2:∠P=90°-∠A;
图3:∠P=∠A;
【推导过程】

以下过程中所用到的∠A、∠B、∠C为原△ABC的三个内角
图1:∠P=180°-(∠1+∠2) =180°-(+) =180°-
=180°-(-)=90°+
图2:∠P=180°-(∠3+∠4) =180°-(+) =180°-
=180°-(+)=90°-
图3:∠P=∠6-∠5=-=
针对以上模型,需注意模型结论适用的条件,并能够理解或熟练展开书写推导过程,再辅以针对练习,最终能够正确应用。

新东方广州学校官方微信号:XDFGZXX
您可以通过公众号菜单栏【找课程】完成在线咨询、课程查询、附近
校区查找、预约试听课等操作。
焦点推荐
版权及免责声明
① 凡本网注明"稿件来源:新东方"的所有文字、图片和音视频稿件,版权均属新东方教育科技集团(含本网和新东方网) 所有,任何媒体、网站或个人未经本网协议授权不得转载、链接、转贴或以其他任何方式复制、发表。已经本网协议授权的媒体、网站,在下载使用时必须注明"稿件来源:新东方",违者本网将依法追究法律责任。
② 本网未注明"稿件来源:新东方"的文/图等稿件均为转载稿,本网转载仅基于传递更多信息之目的,并不意味着赞同转载稿的观点或证实其内容的真实性。如其他媒体、网站或个人从本网下载使用,必须保留本网注明的"稿件来源",并自负版权等法律责任。如擅自篡改为"稿件来源:新东方",本网将依法追究法律责任。
③ 如本网转载稿涉及版权等问题,请作者见稿后在两周内速来电与新东方网联系,电话:010-60908555。